Область устойчивости системы в плоскости одного параметра
Характеристическое уравнение системы имеет вид:
Предположим что параметр А - комплексное число. Заменим 
получим:
Вещественная и мнимая части:
Задавая различные значения 
, вычерчиваем кривую вектора 
, показанную на рис.11. После этого надо наметить предполагаемую область устойчивости. Для этого применяем правило штриховки, основанное на том, что границей в плоскости корней является мнимая ось и при движении по ней от
до
область корней устойчивой системы располагается слева.
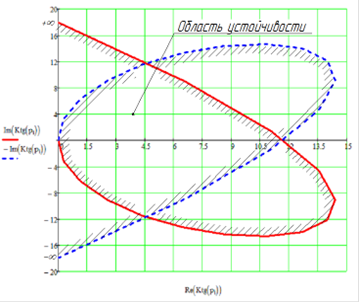
Рис. 11. D - разбиение плоскости комплексного параметра А.
Соответственно этому в плоскости на D - кривой необходимо отметить направление движения в диапазоне частот 
и также заштриховать левую часть кривой по отношению к этому движению. Часть плоскости, в сторону которой направлена штриховка может рассматриваться как предполагаемая область устойчивости.
Взяв из предполагаемой области устойчивости значение 5, проверим по критерию Рауса, устойчива ли система в этой области.
|
Ввод | ||||
|
a0 |
a1 |
a2 |
a3 |
a4 |
|
5 |
1,03 |
0,03075 |
0,00075 |
0,000015625 |
|
r |
c | |||
|
5 |
0,03075 |
0,000015625 |
0 | |
|
1,03 |
0,00075 |
0 |
0 | |
|
4,854368932 |
0,027109223 |
0,000015625 |
0 |
0 |
|
37,99444892 |
0,000156337 |
0 |
0 |
0 |
|
173,4027719 |
0,000015625 |
0 |
0 |
0 |
|
10,00555108 |
0 |
0 |
0 |
0 |
В первом столбце нет ни одной перемены знака, следовательно система устойчива, а данная область действительно является областью устойчивости.
Статья в тему
Строительство новой АМТСЭ на базе оборудования SI-2000
Широкое внедрение цифровой и вычислительной техники в системе
связи обусловило необходимость ориентации и подготовки студентов на
перспективную технику коммутации и управления, на внедрение достижений
микропроцессорной техники в системе коммутации. Данная работа закладывает
фундамент ...