Анализ нескорректированной САУ
Характеристическое уравнение системы имеет вид:
где
.1 По алгебраическим критериям
Критерий Гурвица:
Расчет производим при помощи Excel:
|
Ввод | ||||
|
a0 |
a1 |
a2 |
a3 |
a4 |
|
2 |
0,8 |
0,0201 |
0,0001275 |
0,000003125 |
|
Матрица | ||||
|
0,8 |
0,0001275 |
0 |
0 | |
|
2 |
0,0201 |
0,000003125 |
0 | |
|
0 |
0,8 |
0,0001275 |
0 | |
|
0 |
2 |
0,0201 |
0,000003125 | |
|
Δ1 |
0,8 | |||
|
Δ2 |
0,015825 | |||
|
Δ3 |
1,76875E-08 | |||
|
Δ4 |
5,52734E-14 | |||
Для того чтобы система автоматического управления была устойчива, необходимо и достаточно, чтобы все определители Гурвица были положительны. Так как не все определители больше нуля, то система устойчива.
Критерий Рауса:
Для того, чтобы САУ была устойчива, необходимо и достаточно, чтобы коэффициенты первого столбца таблицы Рауса были одного знака (положительны).
Таблица Рауса составляется следующим образом: в первой строке записывают в порядке возрастания индексов коэффициенты характеристического уравнения, имеющие четный индекс: a0, a2, a4…, во второй строке - коэффициенты с нечетным индексом: a1, a3, a5…
Любой из остальных элементов таблицы определяют как
,
где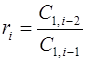 
, k - номер столбца, i - номер строки. Недостающие элементы заменяются нулями.
Определим устойчивость системы автоматического управления по критерию Рауса с помощью Excel:
|
Ввод | ||||
|
a0 |
a1 |
a2 |
a3 |
a4 |
|
2 |
0,8 |
0,0201 |
0,0001275 |
0,000003125 |
|
r |
c | |||
|
2 |
0,0201 |
0,000003125 |
0 | |
|
0,8 |
0,0001275 |
0 |
0 | |
|
2,5 |
0,01978125 |
0,000003125 |
0 |
0 |
|
40,44233807 |
1,11769E-06 |
0 |
0 |
0 |
|
17698,27739 |
0,000003125 |
0 |
0 |
0 |
|
0,357661927 |
0 |
0 |
0 |
0 |
Статья в тему
Системы спутникового мониторинга Глонасс на автотранспорте
Теория нечетких множеств (fuzzy sets theory) ведет свое
начало с 1965г., когда профессор Лотфи Заде (Lotfi Zadeh) из университета
Беркли опубликовал основополагающую работу “Fuzzy Sets” в журнале “Information
and Control”. Прилагательное "fuzzy", которое можно перевест ...