Метод синтеза дискретно-непрерывных систем управления по эталонным моделям движений

Процедура получения вектора неизвестных выглядит следующим образом.

На каждом -ом шаге дискретизации необходимо найти вектор неизвестных . Таким образом на -ом шаге вектор неизвестных равен .

Для ступенчатого управляющего воздействия представляет собой скалярную величину. Для линейного управляющего воздействия представляет собой вектор-столбец размерности 2.

Таким образом на -ом шаге решается система линейных уравнений с ограничениями методом наименьших квадратов размерности 1 для ступенчатого управления или 2 для линейного управления

Сформируем матрицу и вектор , входящие в матричное выражение (5.12), на -ом шаге.

Переходный процесс в моменты дискретизации определяется системой уравнений

(5.14)

В левую часть системы уравнений (5.14) вместо вектора подставим соответствующие значения эталонного переходного процесса . В результате получим выражения для матрицы и вектора :

, .

Формирование матрицы и вектора осуществляется следующим образом. Записываются ограничения (5.13) на управляющее воздействие в виде

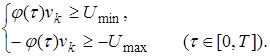(5.15)

При ступенчатом управлении достаточно наложить ограничения сверху и снизу в один момент времени на шаге квантования.

Представим неравенства (5.15) на k-ом шаге с учетом вышесказанного в виде системы неравенств:

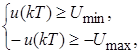
которые с учетом выражений (5.6) можно записать в виде:

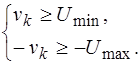
При этом матрица и вектор будут иметь вид:

Статья в тему

Автоматическая спринклерная установка водяного пожаротушения
В современной технике автоматические устройства получили исключительно широкое распространение, так как эффективное использование производственных и других агрегатов, а также разработка новых высокопроизводительных установок становится возможным лишь при передаче функций управления п ...